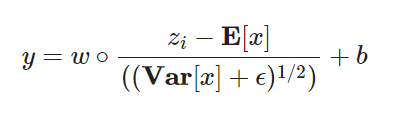cmu 10-414 HW2

Question 2

Xavier uniform

1
2
3
4
5
# 均匀分布 U(-a, a)
def xavier_uniform(fan_in, fan_out, gain=1.0, **kwargs):
    a = gain * math.sqrt(6 / (fan_in + fan_out))
    out = rand(fan_in, fan_out, low=-a, high=a)
    return out

Xavier normal

1
2
3
4
5
# 正太分布 N(0, std)
def xavier_normal(fan_in, fan_out, gain=1.0, **kwargs):
    std = gain * math.sqrt(2 / (fan_in + fan_out))
    out = randn(fan_in, fan_out, mean=0, std=std)
    return out

Kaiming uniform

1
2
3
4
5
6
7
# 均匀分布 U(-bound, bound)
def kaiming_uniform(fan_in, fan_out, nonlinearity="relu", **kwargs):
    assert nonlinearity == "relu", "Only relu supported currently"
    gain = math.sqrt(2)
    bound = gain * math.sqrt(3 / fan_in)
    out = rand(fan_in, fan_out, low=-bound, high=bound)
    return out

Kaiming normal

1
2
3
4
5
6
def kaiming_normal(fan_in, fan_out, nonlinearity="relu", **kwargs):
    assert nonlinearity == "relu", "Only relu supported currently"
    gain = math.sqrt(2)
    std = gain / math.sqrt(fan_in)
    out = randn(fan_in, fan_out, mean=0, std=std)
    return out

Question 2

Linear

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Linear(Module):
    def __init__(
        self, in_features, out_features, bias=True, device=None, dtype="float32"
    ):
        super().__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.have_bias = bias
        
        # weight和bias需要定义成Parameter类型
        self.weight = Parameter(init.kaiming_uniform(in_features, out_features,device = device, dtype = dtype))
        if self.have_bias:
            self.bias = Parameter(init.kaiming_uniform(out_features, 1, device = device, dtype = dtype).reshape((1, out_features)))
        
        

    def forward(self, X: Tensor) -> Tensor:
        if self.have_bias:
            bias = ops.broadcast_to(self.bias, (X.shape[0], self.out_features))
            return ops.matmul(X, self.weight) + bias
        else:
            return ops.matmul(X, self.weight)

Sequential

1
2
3
4
5
6
7
8
9
10
11
class Sequential(Module):
    def __init__(self, *modules):
        super().__init__()
        self.modules = modules
        # print(type(modules))

    def forward(self, x: Tensor) -> Tensor:
        input = x
        for module in self.modules:
            input = module(input)
        return input

LogSumExp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class LogSumExp(TensorOp):
    def __init__(self, axes: Optional[tuple] = None):
        self.axes = axes

    def compute(self, Z): # 再次记住，在进行compute的时候输入输出是array，要使用array_api中的函数
        max_z_f = array_api.max(Z, axis=self.axes, keepdims=False) #和Z的维度一致，每一行中每个元素都是这一行的最大值
        max_z_t = array_api.max(Z, axis=self.axes, keepdims=True) # 公式最后的那个maxz
        tmp = array_api.sum(array_api.exp(Z - max_z_t),axis=self.axes, keepdims=False)
        out = array_api.log(tmp) + max_z_f
        return out

    # 疑问：maxz对z的梯度为0吗，为什么不计算
    def gradient(self, out_grad, node):
        input = node.inputs[0].cached_data
        max_val_t = array_api.max(input, axis=self.axes, keepdims=True)
        exp_val = array_api.exp(input - max_val_t)
        sum_val = array_api.sum(exp_val, axis=self.axes, keepdims=False)
        # log_val = array_api.log(sum_val)
        
        #把log中看成整体，先求对log的梯度
        grad_log = out_grad.cached_data / sum_val 
        
        #求sum的梯度，和summation一样
        shape = list(node.inputs[0].shape)
        axes = self.axes
        if axes is None:
           axes = list(range(len(shape))) #axes为None是对所有维度求和，相当于axes=(0,1,..)
        for _ in axes:
            shape[_] = 1
        grad_sum = array_api.broadcast_to(array_api.reshape(grad_log, shape), node.inputs[0].shape)
        # broadcast_to(reshape(grad_log, shape), node.inputs[0].shape)
        
        #求exp的梯度
        grad_exp = grad_sum * exp_val
        
        return Tensor(grad_exp)

SoftmaxLoss

1
2
3
4
5
6
7
8
9
10
11
class SoftmaxLoss(Module):
    def forward(self, logits: Tensor, y: Tensor):
        softmax = ops.logsumexp(logits, axes=(1,))
        
        shape =  logits.shape
        batch_size = shape[0]
        num_class = shape[1]
        y_one_hot = init.one_hot(num_class, y)
        I = ops.summation(logits * y_one_hot, axes=(1,))
        # print(I)
        return ops.summation(softmax - I) / batch_size

LayerNorm1d

为什么需要Normalization？

深度神经网络模型的训练为什么会很困难？其中一个重要的原因是，深度神经网络涉及到很多层的叠加，而每一层的参数更新会导致上层的输入数据分布发生变化，通过层层叠加，高层的输入分布变化会非常剧烈，这就使得高层需要不断去重新适应底层的参数更新。为了训好模型，我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。Google 将这一现象总结为 Internal Covariate Shift，简称 ICS.

大家都知道在统计机器学习中的一个经典假设是“源空间（source domain）和目标空间（target domain）的数据分布（distribution）是一致的”。如果不一致，那么就出现了新的机器学习问题，如 transfer learning / domain adaptation 等。而 covariate shift 就是分布不一致假设之下的一个分支问题，它是指源空间和目标空间的条件概率是一致的，但是其边缘概率不同，即：对所有𝑥∈𝑋,𝑃𝑠(𝑌|𝑋=𝑥)=𝑃𝑡(𝑌|𝑋=𝑥) 但是𝑃𝑠(𝑋)≠𝑃𝑡(𝑋) 大家细想便会发现，的确，对于神经网络的各层输出，由于它们经过了层内操作作用，其分布显然与各层对应的输入信号分布不同，而且差异会随着网络深度增大而增大，可是它们所能“指示”的样本标记（label）仍然是不变的，这便符合了covariate shift的定义。由于是对层间信号的分析，也即是“internal”的来由。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
"""
开始时计算E时，想直接使用.data来计算，不想创建复杂的计算图。后来意识到这计算过程就是需要创建计算图的。乐
"""
class LayerNorm1d(Module):
    def __init__(self, dim, eps=1e-5, device=None, dtype="float32"):
        super().__init__()
        self.dim = dim
        self.eps = eps
        # 初始化参数
        self.weight = Parameter(init.ones(dim, device=device, dtype=dtype))
        self.bias = Parameter(init.zeros(dim, device=device, dtype=dtype))

    def forward(self, x: Tensor) -> Tensor:
        batch_size = x.shape[0]
        features = x.shape[1]
        
        # 计算均值
        sum_x = ops.summation(x, 1) #计算完后维度降低了,原来是(batch_size, features)现在是(batch_size,)
        mean_x = ops.divide_scalar(sum_x, features)
        mean_x_reshape = ops.reshape(mean_x, (-1,1))

        E = ops.broadcast_to(mean_x_reshape, x.shape)

        # 计算标准差
        V_inner = ops.power_scalar(x-E, 2)
        V_sum = ops.summation(V_inner, 1)   # (batch_size,)
        V_mean = ops.divide_scalar(V_sum, features)
        V = ops.add_scalar(V_mean, self.eps)
        sqrt_Var = ops.power_scalar(V, 1/2)    # (batch_size,)
        sqrt_Var_reshape = ops.reshape(sqrt_Var, (-1,1))
        sqrt_Var_reshape_brocst = ops.broadcast_to(sqrt_Var_reshape, x.shape) # (batch_size,feature)
        
        # 计算X
        X  = (x - E) / sqrt_Var_reshape_brocst
        
        # weight和bias的维度都是dim即features
        broadcast_weight = ops.broadcast_to(ops.reshape(self.weight, (1, -1)), x.shape)
        broadcast_bias = ops.broadcast_to(ops.reshape(self.bias, (1,-1)), x.shape)
        
        out = broadcast_weight * X + broadcast_bias
        return out

BatchNorm1d

image-20240724101503540

LayerNormalize是在一个sample中对所有dimension进行的。而BatchNormalize是针对一个dim将minibatch中该dim所有的值进行规范

image-20240724101916737

公式分两步：

  • 中间的计算使得第 𝑙 层的输入每个特征的分布均值为0，方差为1。
  • 引入可学习的参数w和b，引入的目的是为了恢复数据本身的表达能力，对规范化后的数据进行线性变换

在训练模型时，在每一层计算的 𝜇 与 𝜎2 都是基于当前batch中的训练数据；而当做预测时，一批预测只有一个或者很少样本，计算出的𝜇 与 𝜎2 一定有偏差。如何解决？

保留每组mini-batch训练数据在网络中每一层的 𝜇𝑏𝑎𝑡𝑐ℎ 与 𝜎𝑏𝑎𝑡𝑐ℎ2 。预测时使用整个样本的统计量来对预测数据进行归一化。即额外计算每层网络的运行时均值和方差

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class BatchNorm1d(Module):
    def __init__(self, dim, eps=1e-5, momentum=0.1, device=None, dtype="float32"):
        super().__init__()
        self.dim = dim
        self.eps = eps
        self.momentum = momentum
        
        self.weight = Parameter(init.ones(dim, device=device, dtype=dtype))
        self.bias = Parameter(init.zeros(dim, device=device, dtype=dtype))
        """
        下边两个并不是Parameter，因为他们不是权重，在最后一个测试时发现
        """
        self.running_mean = init.zeros(dim, device=device, dtype=dtype) #运行时每一dim上的均值方差
        self.running_var = init.ones(dim, device=device, dtype=dtype)

    def forward(self, x: Tensor) -> Tensor:
        batch_size = x.shape[0]
        broadcast_weight = ops.broadcast_to(ops.reshape(self.weight, (1, -1)), x.shape)
        broadcast_bias = ops.broadcast_to(ops.reshape(self.bias, (1,-1)), x.shape)
        
        if self.training:    
        # 计算当前batch的均值
            sum_x = ops.summation(x, 0) #(batch_size, features)->(features)
            mean_x = ops.divide_scalar(sum_x, batch_size)
            broadcast_mean = ops.broadcast_to(mean_x, x.shape)

            # 计算当前batch的标准差
            pow_Var = ops.power_scalar(x-broadcast_mean, 2)
            sum_Var = ops.summation(pow_Var, 0) #(batch_size, features)->(features)
            Var = ops.divide_scalar(sum_Var, batch_size)
            Var_add_eps = ops.power_scalar(ops.add_scalar(Var, self.eps), 1/2)
            broadcast_var = ops.broadcast_to(Var_add_eps, x.shape)
            
            out = broadcast_weight * (x - broadcast_mean) / broadcast_var + broadcast_bias
            
            self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * mean_x
            self.running_var = (1 - self.momentum) * self.running_var + self.momentum * Var
        else:
            broadcast_running_mean = ops.broadcast_to(ops.reshape(self.running_mean, (1,-1)), x.shape)
            running_var_add_eps = ops.power_scalar(ops.add_scalar(self.running_var, self.eps), 1/2)
            broadcast_running_var = ops.broadcast_to(ops.reshape(running_var_add_eps, (1,-1)), x.shape)
            out = broadcast_weight * (x-broadcast_running_mean) / broadcast_running_var + broadcast_bias
        
        return out

Dropout

1
2
3
4
5
6
7
8
9
10
class Dropout(Module):
    def __init__(self, p=0.5):
        super().__init__()
        self.p = p

    def forward(self, x: Tensor) -> Tensor:
        if self.training:
            mask = init.randb(*x.shape, p = 1- self.p) / (1 - self.p)
            x = x * mask
        return x

Residual

1
2
3
4
5
6
7
class Residual(Module):
    def __init__(self, fn: Module):
        super().__init__()
        self.fn = fn

    def forward(self, x: Tensor) -> Tensor:
        return self.fn(x) + x

Question3

SGD

有几个需要注意的

  • u是字典，key是Param，value是该Param上一次计算时的梯度。
  • weight_decay表明需要考虑L2regularization，即真正的梯度是param.grad.data + weight_decay * W，这才是(1-β)后的那个梯度
  • 因为写完后报错float64和float32不一致，所以将grad的dtype改成param的dtype
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class SGD(Optimizer):
    def __init__(self, params, lr=0.01, momentum=0.0, weight_decay=0.0):
        super().__init__(params) # params是包含多个需要进行多次迭代计算的Param
        self.lr = lr
        self.momentum = momentum
        self.u = {} # 字典，key是Param，value是该Param上一次计算时的梯度
        self.weight_decay = weight_decay

    def step(self):
        for param in self.params:
            grad  = self.u.get(param, 0) * self.momentum + (1-self.momentum) * (param.grad.data + self.weight_decay * param.data)
            grad = ndl.Tensor(grad, dtype = param.dtype)
            self.u[param] = grad
            param.data =  param.data - self.lr * grad

Adam

增加 if param.grad is not None:判断条件是因为报错param.grad是NoneType的情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Adam(Optimizer):
    def __init__(
        self,
        params,
        lr=0.01,
        beta1=0.9,
        beta2=0.999,
        eps=1e-8,
        weight_decay=0.0,
    ):
        super().__init__(params)
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.eps = eps
        self.weight_decay = weight_decay
        self.t = 0

        self.m = {}
        self.v = {}

    def step(self):
        self.t += 1
        for param in self.params:
            if param.grad is not None:
                grad_with_L2rgl = param.grad.data + self.weight_decay * param.data
            else:
                grad_with_L2rgl = self.weight_decay * param.data
            new_m = self.beta1 * self.m.get(param, 0) + (1-self.beta1) * grad_with_L2rgl.data
            new_v = self.beta2 * self.v.get(param, 0) + (1-self.beta2) * grad_with_L2rgl.data * grad_with_L2rgl.data
            self.m[param] = new_m
            self.v[param] = new_v
            m_hat = new_m.data / (1 - self.beta1 ** self.t)
            v_hat = new_v.data / (1 - self.beta2 ** self.t)
            out = param.data - self.lr * m_hat / (ndl.ops.power_scalar(v_hat, 1/2) + self.eps)
            out = ndl.Tensor(out, dtype=param.dtype)
            param.data = out

Question4

Transformations

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class RandomFlipHorizontal(Transform):
    def __init__(self, p = 0.5):
        self.p = p

    def __call__(self, img):
        """
        Horizonally flip an image, specified as an H x W x C NDArray.
        Args:
            img: H x W x C NDArray of an image
        Returns:
            H x W x C ndarray corresponding to image flipped with probability self.p
        Note: use the provided code to provide randomness, for easier testing
        """
        flip_img = np.random.rand() < self.p
        if flip_img:
            img = img[:,::-1,:]
        return img
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class RandomCrop(Transform):
    def __init__(self, padding=3):
        self.padding = padding

    def __call__(self, img):
        """ Zero pad and then randomly crop an image.
        Args:
             img: H x W x C NDArray of an image
        Return 
            H x W x C NAArray of cliped image
        Note: generate the image shifted by shift_x, shift_y specified below
        """
        shift_x, shift_y = np.random.randint(low=-self.padding, high=self.padding+1, size=2) # [-self.padding, self.padding]
        H, W, C = img.shape
        pad = np.zeros((H+2*self.padding, W+2*self.padding, C))
        pad[self.padding:self.padding+H,self.padding:self.padding+W,:] = img
        x = shift_x + self.padding
        y = shift_y + self.padding
        img = pad[x:x+H, y:y+W,:]
        return img

MNISTDataset

Dataset的作用是对于给定的数据路径，读取其中的数据

  • parse_mnist是从hw0复制来的，但是由于上边的转换函数我们发现对于一个sample是H* W* C，因此输出的X的维度应该是(sample_numbles, H, W, C)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class MNISTDataset(Dataset):
    def __init__(
        self,
        image_filename: str,
        label_filename: str,
        transforms: Optional[List] = None,
    ):
        self.images, self.labels = parse_mnist(image_filename, label_filename)
        self.transforms = transforms


    def __getitem__(self, index) -> object:
        img = self.images[index]
        return self.apply_transforms(img), self.labels[index]

    def __len__(self) -> int:
        return self.images.shape[0]
# copy from hw0
def parse_mnist(image_filename, label_filename):
    with gzip.open(image_filename, 'rb') as img_f:
        img_f.read(4) #skip magic number
        num_images = int.from_bytes(img_f.read(4), 'big') # stored by high(big) endian
        rows = int.from_bytes(img_f.read(4), 'big')
        cols = int.from_bytes(img_f.read(4), 'big')
        
        image_data = img_f.read(num_images * rows * cols)
        X = np.frombuffer(image_data, dtype=np.uint8).astype(np.float32)
        X = X.reshape(num_images, rows, cols, 1) #(sample_numbles, H, W, C)
        X /= 255.0 # normalize to [0,1]
        
    with gzip.open(label_filename, 'rb') as lb_f:
        lb_f.read(4)
        num_labels = int.from_bytes(lb_f.read(4), 'big')
        
        lable_data = lb_f.read(num_labels)
        y = np.frombuffer(lable_data, dtype=np.uint8)
    return X, y

Dataloader

给定Dataset，将数据按batch_size进行分批，并通过iter和next实现迭代。每次训练输入一批数据。需要注意一个坑：shuffle表示数据集中的sample是否需要打乱。开始时我直接在init()函数中判断，如果为true，直接做数据的打乱，而在iter函数中直接return self代码如下

1
2
3
4
5
6
7
8
9
if not self.shuffle:
	self.ordering = np.array_split(np.arange(len(dataset)), 
                                           range(batch_size, len(dataset), batch_size))
else:
	self.ordering = np.array_split(np.random.permutation(len(self.dataset)), 
                                           range(self.batch_size, len(self.dataset), self.batch_size))

def __iter__(self):
    return self

而这么做的问题是，一旦在init中打乱，那么当做多epoch的训练时，对于不同的epoch来说，其ordering中的minibatch是一样的，因为只打乱了一次。

因此不能再init中打乱，而需要在iter中打乱。这样在每个epoch中，对minibatch的迭代开始时调用一次iter，到下一个epoch时，对minibatch迭代会再次调用iter，保证不同epoch中minibatch都不同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class DataLoader:
    r"""
    Data loader. Combines a dataset and a sampler, and provides an iterable over
    the given dataset.
    Args:
        dataset (Dataset): dataset from which to load the data.
        batch_size (int, optional): how many samples per batch to load
            (default: ``1``).
        shuffle (bool, optional): set to ``True`` to have the data reshuffled
            at every epoch (default: ``False``).
     """
    dataset: Dataset
    batch_size: Optional[int]

    def __init__(
        self,
        dataset: Dataset,
        batch_size: Optional[int] = 1,
        shuffle: bool = False,
    ):

        self.dataset = dataset
        self.shuffle = shuffle
        self.batch_size = batch_size
        if not self.shuffle:
            self.ordering = np.array_split(np.arange(len(dataset)), 
                                           range(batch_size, len(dataset), batch_size))
        
    def __iter__(self):
        if self.shuffle:
            self.ordering = np.array_split(np.random.permutation(len(self.dataset)), 
                                           range(self.batch_size, len(self.dataset), self.batch_size))
        self.idx = -1
        return self
    def __next__(self):
        self.idx += 1
        if self.idx >= len(self.ordering):
            self.idx = -1
            raise StopIteration()
        samples = self.dataset[self.ordering[self.idx]]
        samples = [Tensor(s) for s in samples]
        return samples

Question 5

ResidualBlock

1
2
3
4
5
6
7
8
9
10
def ResidualBlock(dim, hidden_dim, norm=nn.BatchNorm1d, drop_prob=0.1):
    main = nn.Sequential(
        nn.Linear(dim, hidden_dim),
        norm(hidden_dim),
        nn.ReLU(),
        nn.Dropout(drop_prob),
        nn.Linear(hidden_dim, dim),
        norm(dim),
    )
    return nn.Sequential(nn.Residual(main), nn.ReLU())

MLPResNet

作业的图中是没用Flatten的，但是输入的X的dim是(batch_size, H, W, C), 而第一个W的维度是(dim, hidden_dim),这里的dim=H* W* 1。因此要给X进行Flatten

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def MLPResNet(
    dim,
    hidden_dim=100,
    num_blocks=3,
    num_classes=10,
    norm=nn.BatchNorm1d,
    drop_prob=0.1,
):
    layers = []
    layers.append(nn.Flatten())
    layers.append(nn.Linear(dim, hidden_dim))
    layers.append(nn.ReLU())
    for i in range(num_blocks):
        layers.append(ResidualBlock(hidden_dim, hidden_dim // 2, norm, drop_prob))
    layers.append(nn.Linear(hidden_dim, num_classes))
    return nn.Sequential(*layers)

Epoch

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def epoch(dataloader, model, opt=None): # opt是优化器，如SGD， Adam
    np.random.seed(4)
    if opt is None:
        model.eval()
    else:
        model.train()
    loss_fuc = nn.SoftmaxLoss()
    acc_num = 0
    losses = []
    for X, y in dataloader:
        out = model(X)
        loss = loss_fuc(out, y)
        if opt is not None:
            loss.backward() #计算节点梯度
            opt.step() #权重更新
            
        losses.append(loss.numpy())
        acc_num += (out.numpy().argmax(axis=1) == y.numpy()).sum()
        
    return 1 - acc_num / len(dataloader.dataset), np.mean(losses)

Train Mnist

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def train_mnist(
    batch_size=100,
    epochs=10,
    optimizer=ndl.optim.Adam,
    lr=0.001,
    weight_decay=0.001,
    hidden_dim=100,
    data_dir="data",
):
    np.random.seed(4)
    #  Initialize tranning dataloader
    trainning_dataset = ndl.data.MNISTDataset(
        os.path.join(data_dir, "train-images-idx3-ubyte.gz"),
        os.path.join(data_dir, "train-labels-idx1-ubyte.gz")
    )
    trainning_data_loader = ndl.data.DataLoader(trainning_dataset, batch_size, shuffle=True)
    #  Initialize test dataloader
    test_dataset = ndl.data.MNISTDataset(
        os.path.join(data_dir, "t10k-images-idx3-ubyte.gz"),
        os.path.join(data_dir, "t10k-labels-idx1-ubyte.gz")
    )
    test_data_loader = ndl.data.DataLoader(test_dataset, batch_size)

    shape = test_data_loader.dataset.images.shape
    dim = shape[1] * shape[2]
    print(dim)
    model = MLPResNet(dim=dim, hidden_dim=hidden_dim)

    opt = optimizer(model.parameters(), lr=lr, weight_decay=weight_decay)

    train_err,train_loss = 0, 0
    test_err,test_loss = 0, 0

    for i in range(epochs):
        train_err, train_loss = epoch(trainning_data_loader, model, opt)
        print("Epoch %d: Train err: %f, Train loss: %f" % (
            i, train_err, train_loss
        ))
    test_err, test_loss = epoch(test_data_loader, model)
    return train_err, train_loss, test_err, test_loss